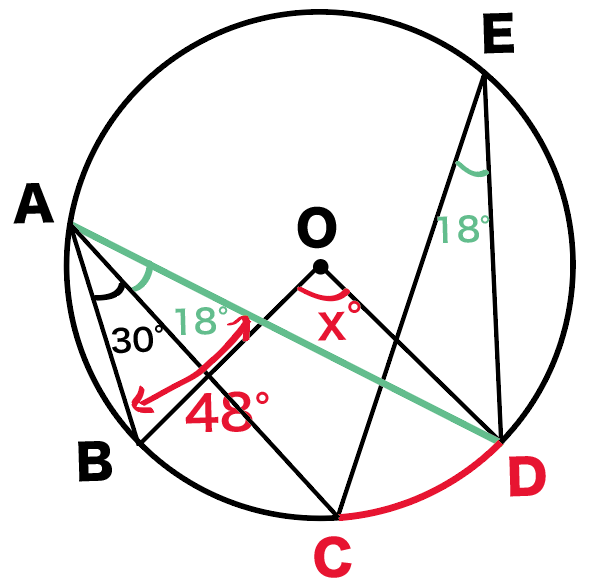
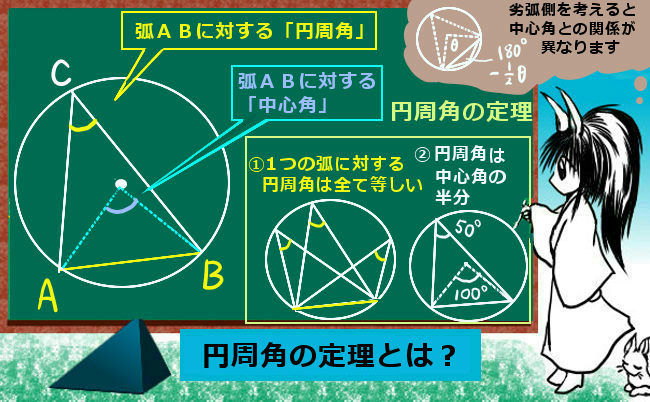
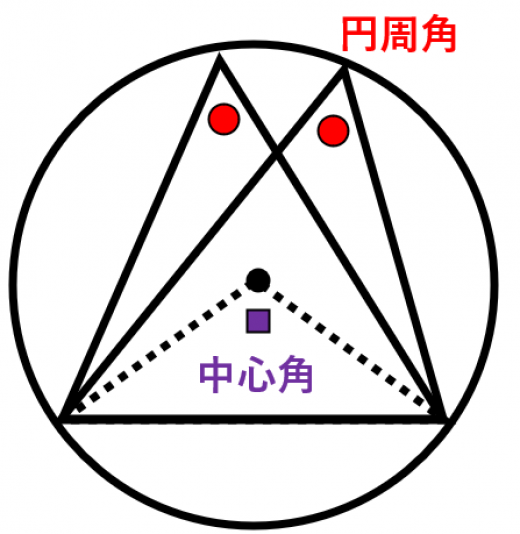
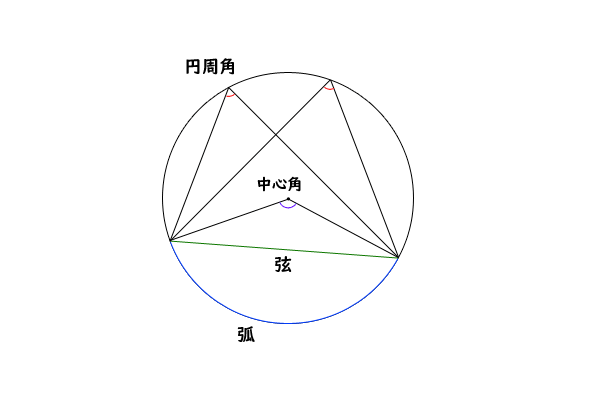
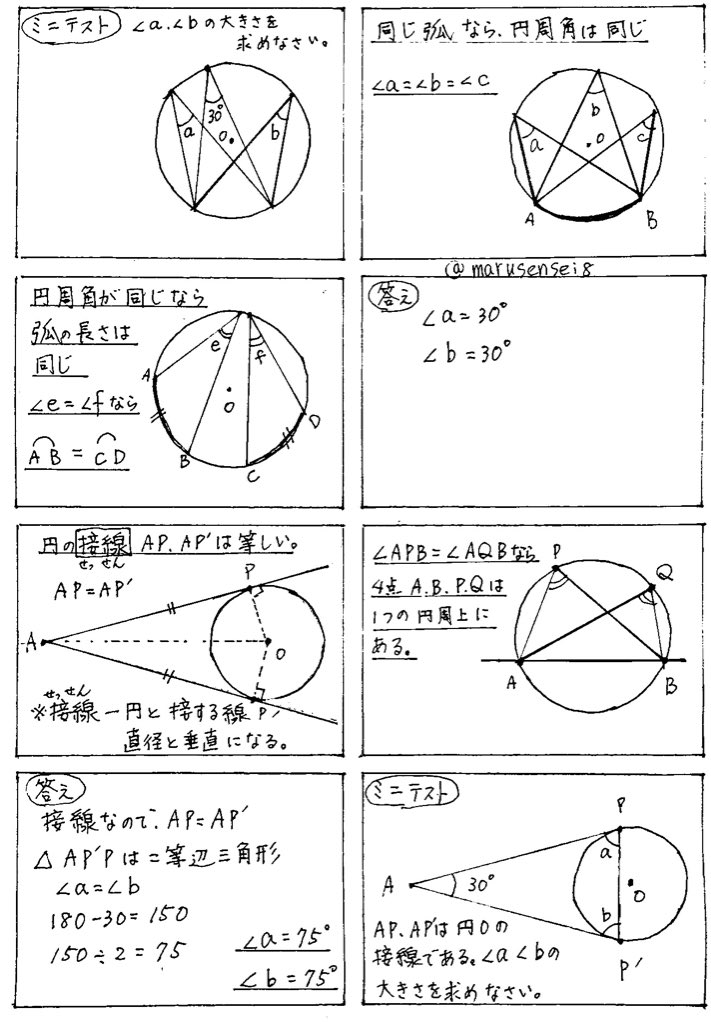
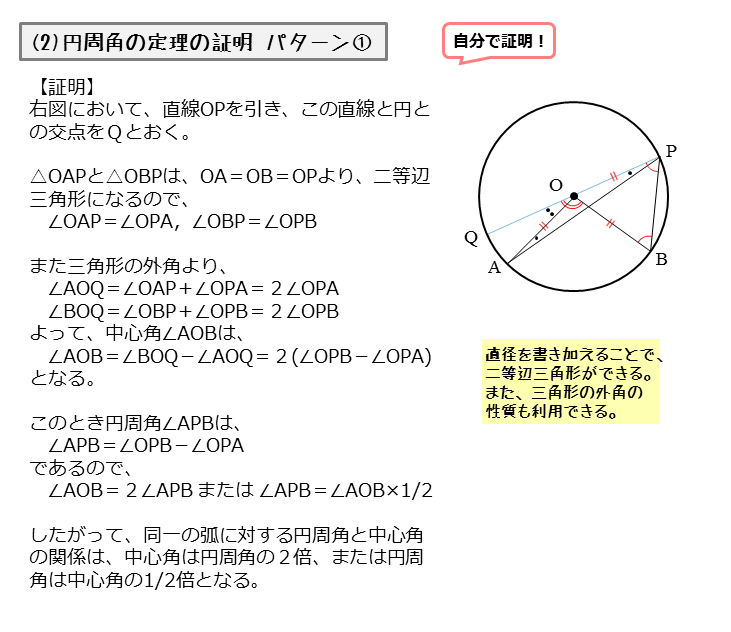
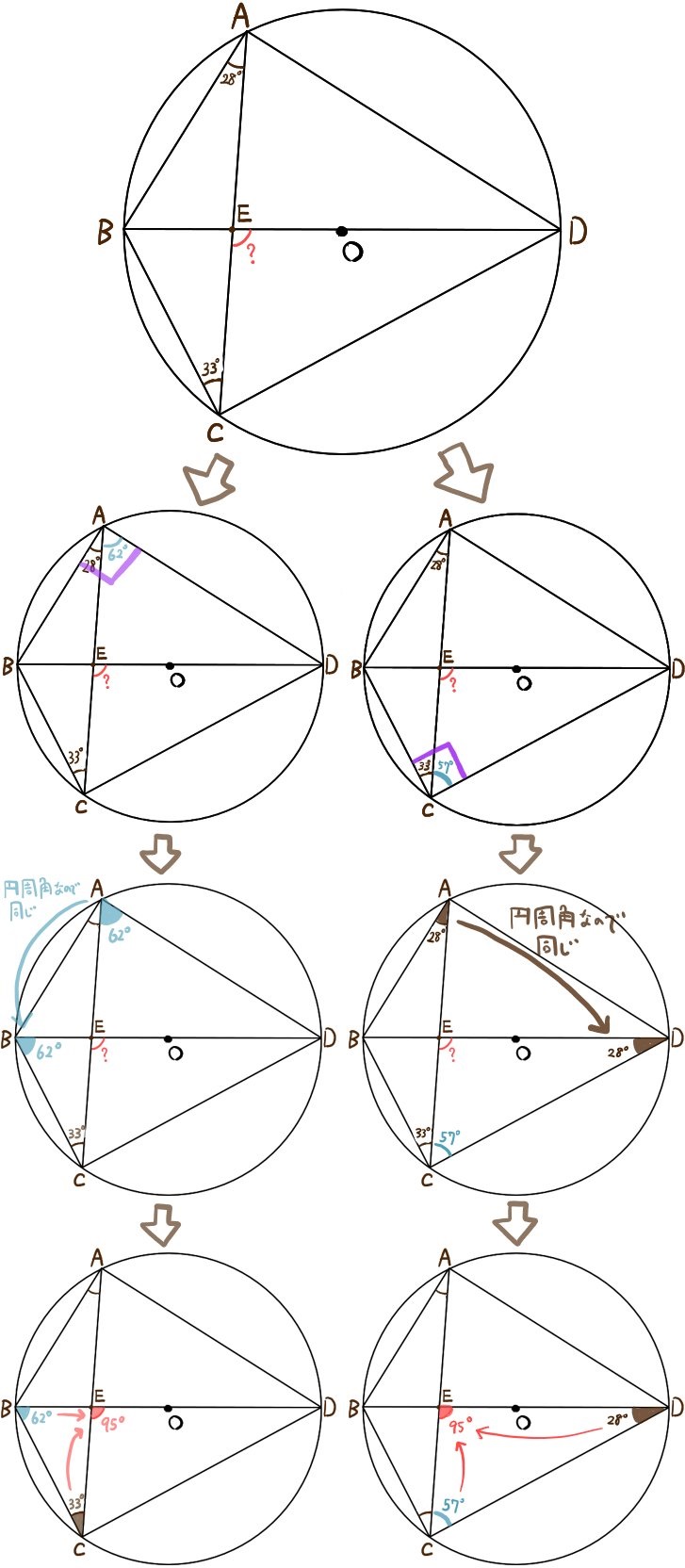
円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135° 2 135 ° 2 = 675° 同様に、yは2コマ分の中心角の半分 → y = 1 2 1 2 (2×45°) = 90° 2 90 ° 2 = 45° 同じ弧より
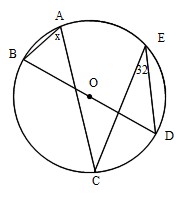
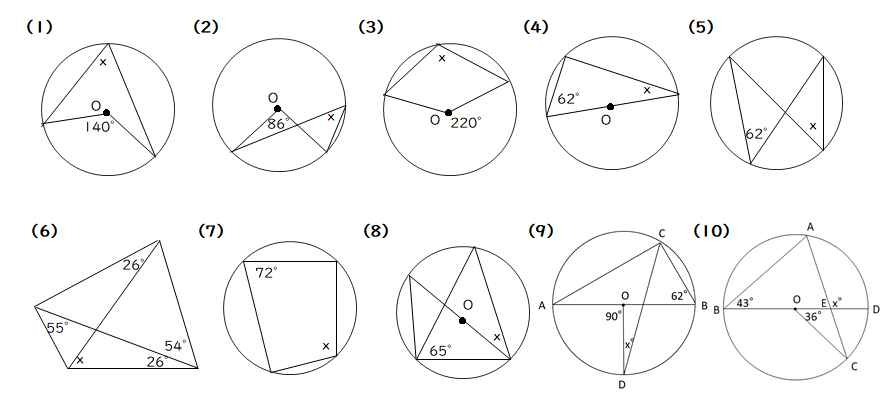
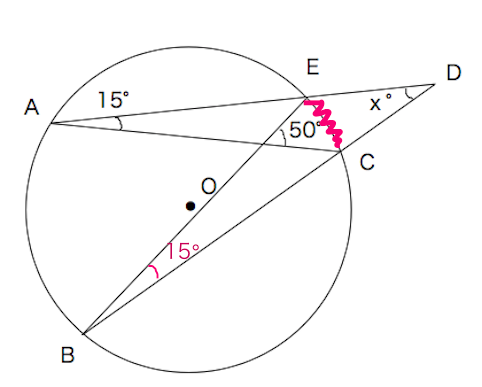
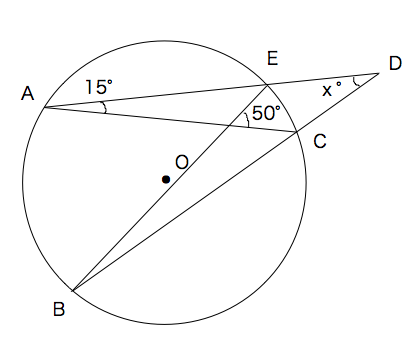
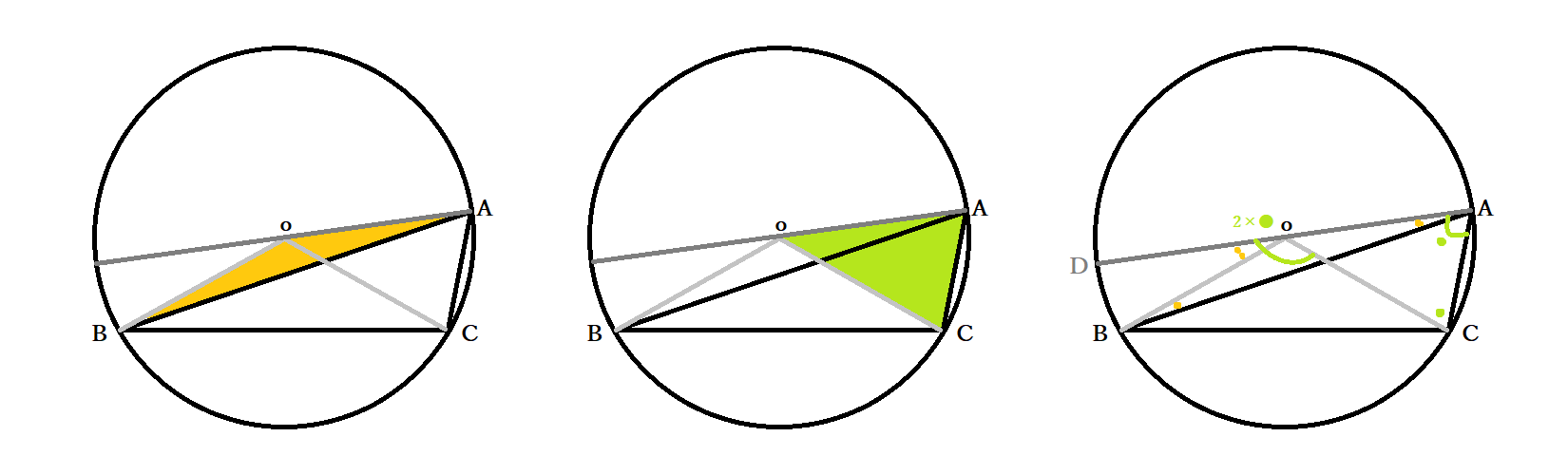
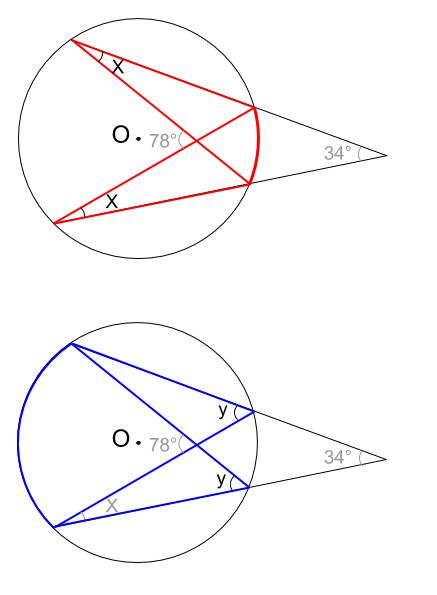
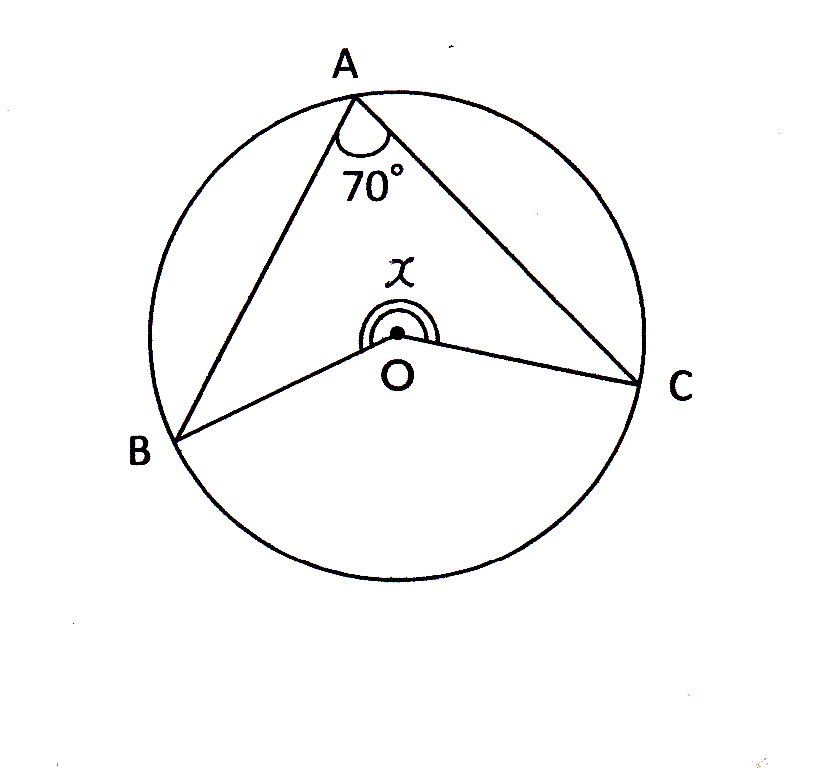
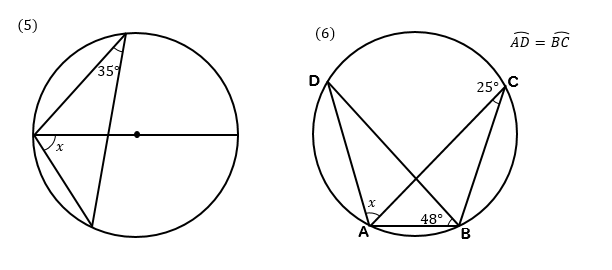
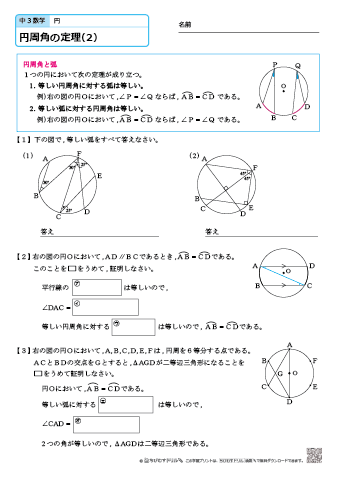
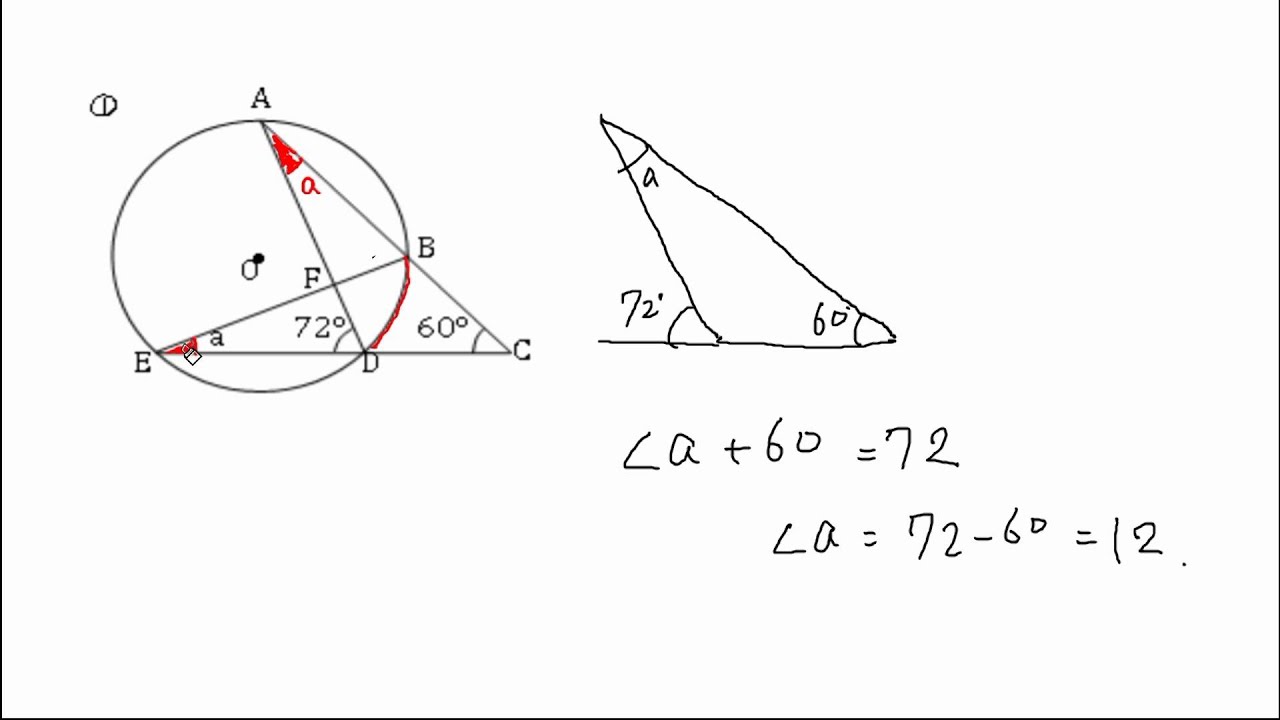
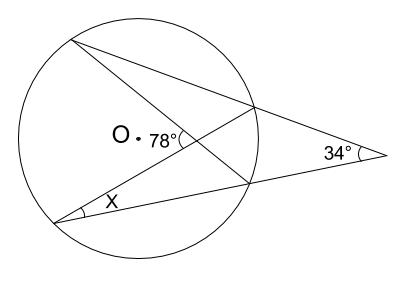
円周角の定理 問題 高校-円周角1 それぞれのxの値を求めよ。 ただし、点Oは円の中心である。 78° x O x O 56° 49° x O O 62° x x O 132° 6° x O O x 128° 109° x O x 28° x 102° x 18° 24° O ° 30° x ①の解説 ②③④⑤⑨の解説 ⑥⑧の解説 ⑦の解説 ⑩の解説 ⑪の解説 ⑫の解説一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 一つの弧に対する円周角は等しい. (2) 三角形の内角の和は180°になる. 問題2 (1) 右の図のよう
円周角の定理 問題 高校のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  | |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 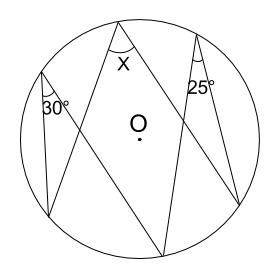 | |
 |  | |
 | 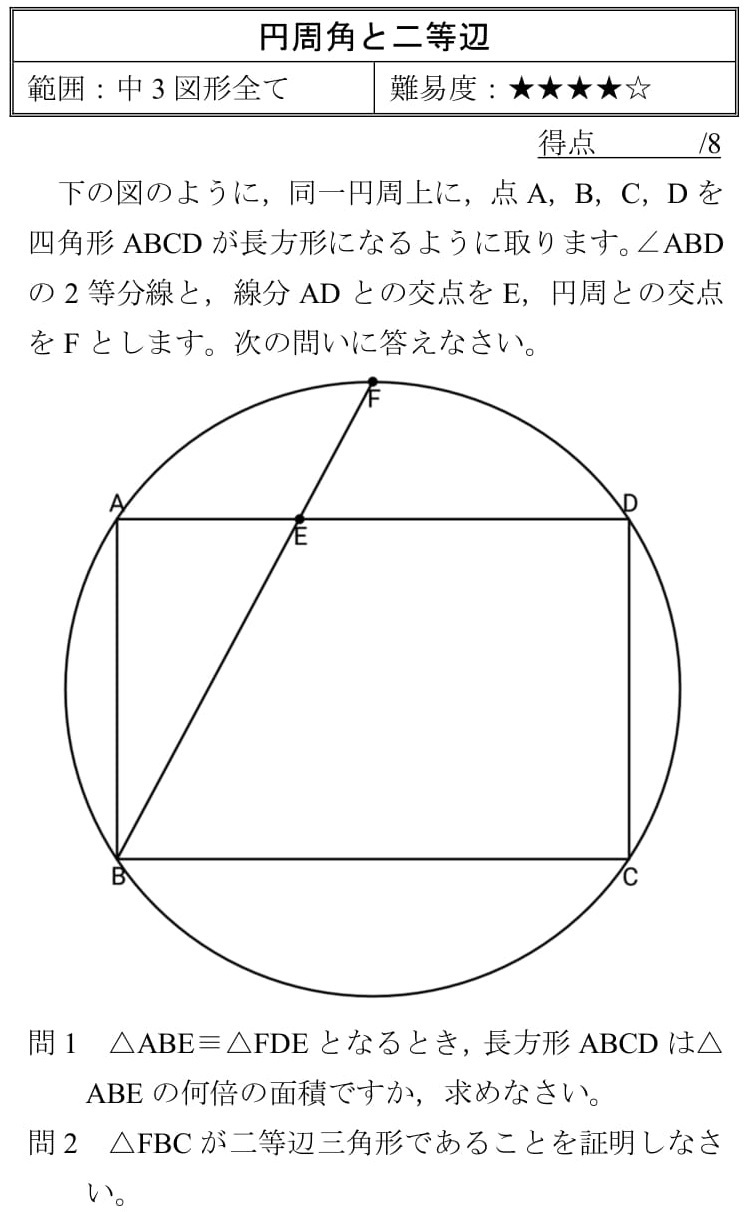 | |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 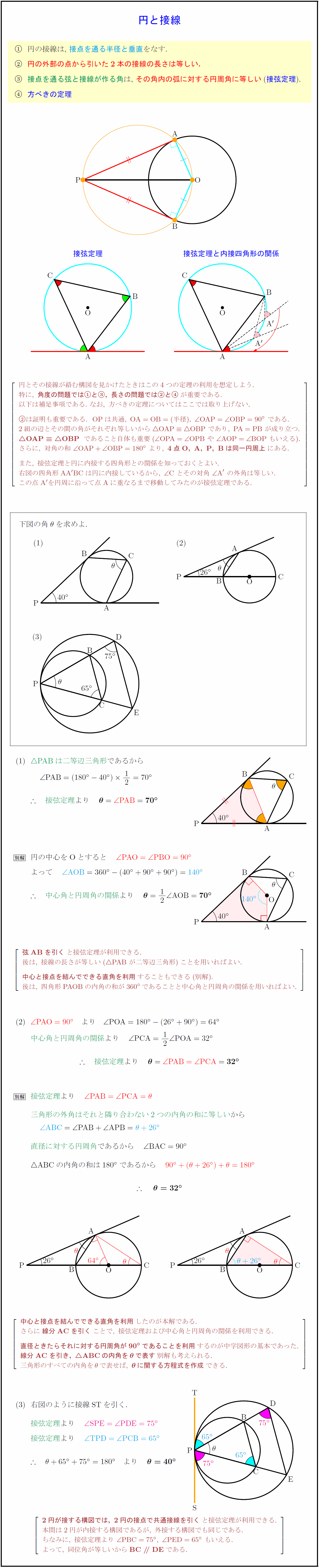 | |
 |  | |
 |  | |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  | |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「円周角の定理 問題 高校」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
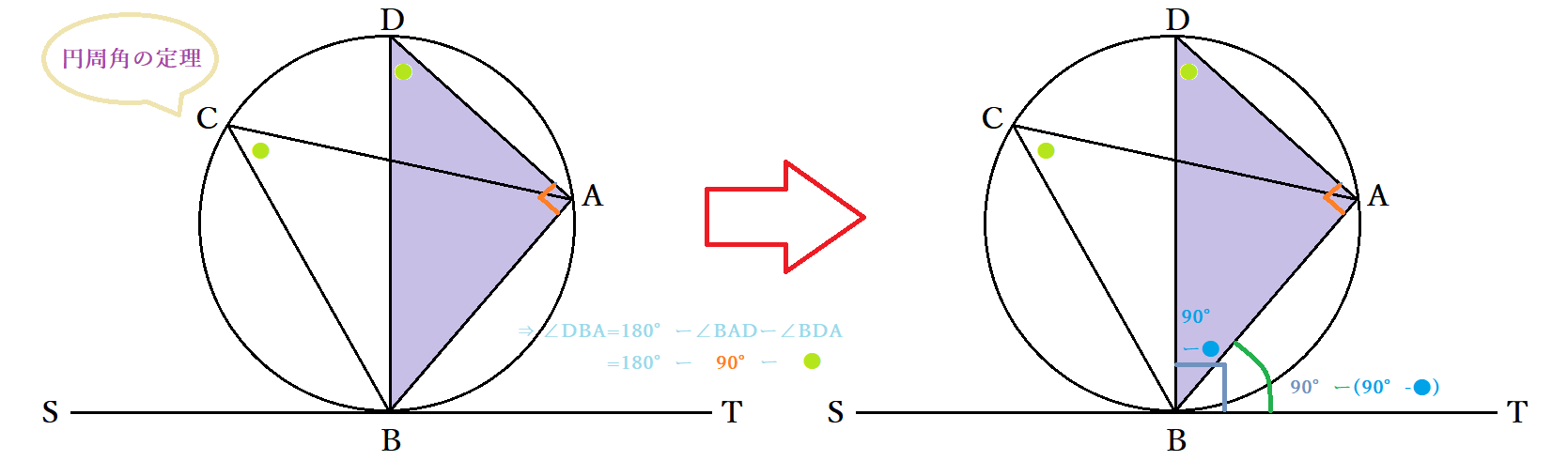
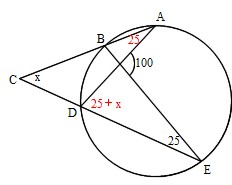
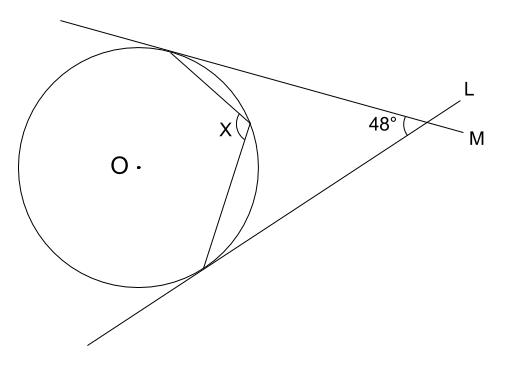
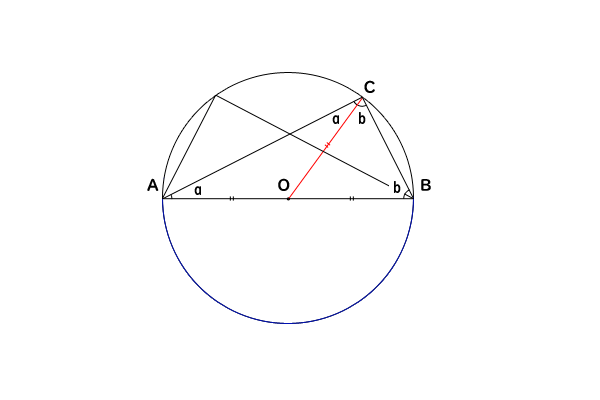
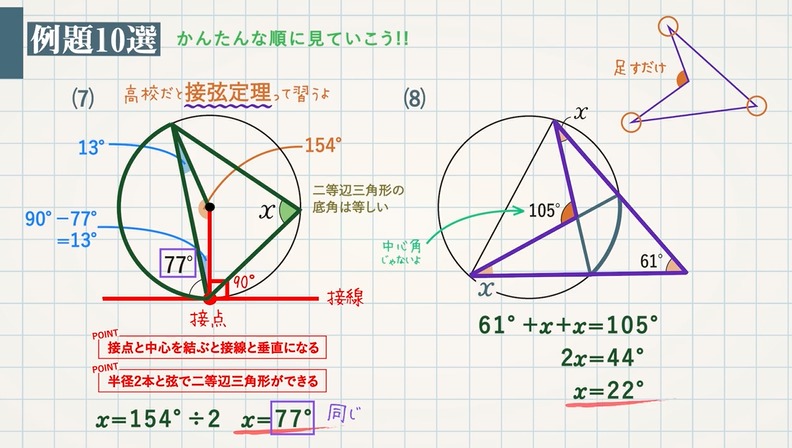
求める角は円周角50°に対応する中心角だから100 接弦定理を使って イの図 で考えるとき 「接線ATと弦APがなす角∠PATは,その内部にある弧APに対する円周角∠ABPに等しい」から∠ABP=60°.したがって,∠ABO=40°.半径を2辺とする二等辺三角形の両底角は 円周角の定理の逆とは? 次に、「円周角の定理の逆」について説明します。 逆って何?と思った方もいるでしょう。「円周角の定理の逆」とは、 図で表すと、以下のときは、 a,b,p,qが円周上にある、ということです。 なぜこうなるのか説明する前に、





0 件のコメント:
コメントを投稿