直角三角形で、斜辺の長さをc、残りの辺の長さをa, b (a 3辺の長さが3:4:5の三角形は直角三角形だということをご存じの方も多いと思いますが、その他の整数比の直角三角形は?、と言われてパッと思いつくでしょうか?力の分解(三角比編) 本編で力の分解を扱ったとき,分力の大きさは直角三角形の辺の比を用いて計算していました。 力の合成・分解 力学では物体の運動と力の関係を調べることがメインテーマになります。 そのとき必要になる「力の取り扱い方」を 平行線+三角形の相似 辺の比と相似のテクニック2つ! 辺の比と連比はテクニック2つ!(共通の辺を2つの比で→最小公倍数で揃える) 直角三角形の相似(「3:4:5」「5:12:13」) ピタゴラス数:直角三角形の基本(3:4:5)
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web
直角三角形 辺の比 小学生
直角三角形 辺の比 小学生- 3:4:5の三角形で,本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角です。このことは,三平方の定理として知られています。 3:4:5直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは,1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理(ピタゴラスの定理)



Tossランド 特別な直角三角形の辺の比の復習のさせ方
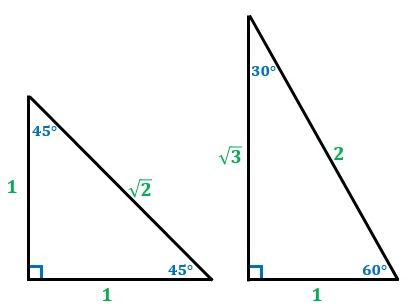
三角比 sin30°, cos45°, tan60° の値を求めなさい。 1つの角が 30° である直角三角形の辺の比は 1∶2∶√3 となっているので,sin30°= 1 2 また,1つの角が 60° である直角三角形の辺の比も 様なの 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な直角をはさむ2辺の長さは同じ です。 辺の長さの比1:1:√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です。
直角二等辺三角形の辺の比は、必ず「 \color {red} {1 1 \sqrt {2}} 」 となります。 1 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。 なぜこの比が成り立つかは、 三平方の定理 から示すことができます。 三平方の直角三角形を使って考えると、鋭角(0°< θ <90°)の場合の三角比しか考えられません。 しかし、座標にあてはめて考えることで鈍角(90直角三角形の辺の長さを求める問題(三角測量の問題)においては,必要な三角比の値が分かっていなければなりませんが,次の3種類×3の値は問題文に書かれていなくても読者が覚えていなければなりません. これ以外の値,例えば sin 22°などが必要に
直角三角形の角度と、長さの比 数学Ⅰの第3章 「三角比」 について学習していこう。 三角比とは、 直角三角形の比 を表す値だよ。 直角三角形 って、 あるもの が決まると、 辺の長さの比 が1つに決まるんだよ。 中学校で勉強した内容だけれど、覚えて 1 数学三角形の辺と面積の比について、2つの考え方をサクッとまとめました中学数学 図形 11 三角形の線分比と面積比の関係①;直角三角形を作る! (2) の値を求めよ。 36°の三角比の値を求めるためには、36°の角を含む直角三角形を作ってやることがポイントです。 (1)で求めた辺の大きさを利用できる直角三角形を次のように作ってやります。 そして、この直角三角形の斜辺



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三角比は直角三角形が基本 理系男子の独り善がり
直角三角形abcにおいては、 bd:dc=ab²:ac² でした。 したがって、 bd:dc=169:81 です。 2乗すればいいだけですね。簡単です。 三平方の定理など他にもいくつかの方法で解くことができますが、これを知っていれば数秒で終わります。直角三角形である。 (2) 9cm, 8cm, 4cm 9が最も長いのでc 2 = 81 a 2 b 2 = 64 16 =80 よってa 2 b 2 ≠ c 2 となるので 直角三角形ではない。 確認 次の長さを3辺とする三角形のうち、直角三角形をすべて選べ。 答表示直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に




特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてください Clear
中点連結定理 a b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2)実は,上記の三角形 A B C ABC A BC は正五角形の3つの頂点となっています。 x x x は1辺の長さが1の正五角形の対角線の長さを表しており,有名な黄金比が登場します。 トレミーの定理を使って求めることもできます。 直角三角形の合同条件には、以下の 2 つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい 1 つの角が 90^\circ であることから、斜辺の長さおよび 1 つの鋭角が等しいことが示せれば、 残りの 1 角も自ずと定まります 。



Tossランド 特別な直角三角形の辺の比の復習のさせ方



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん
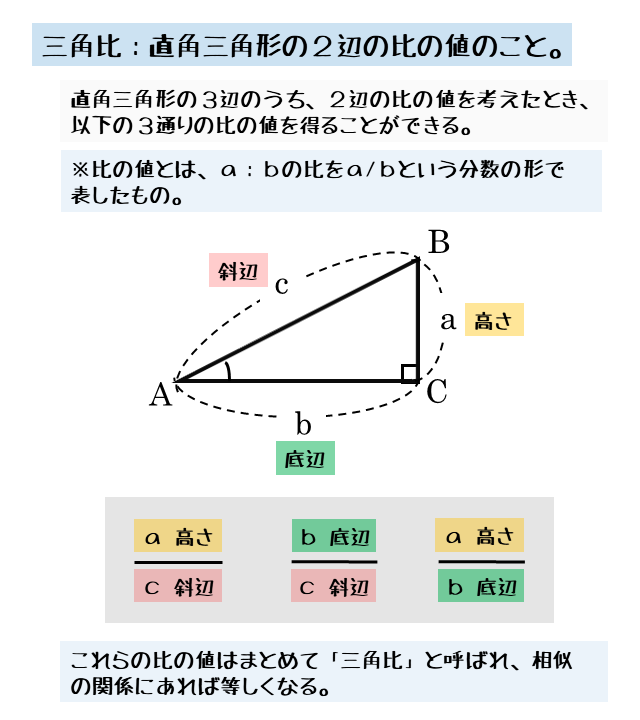
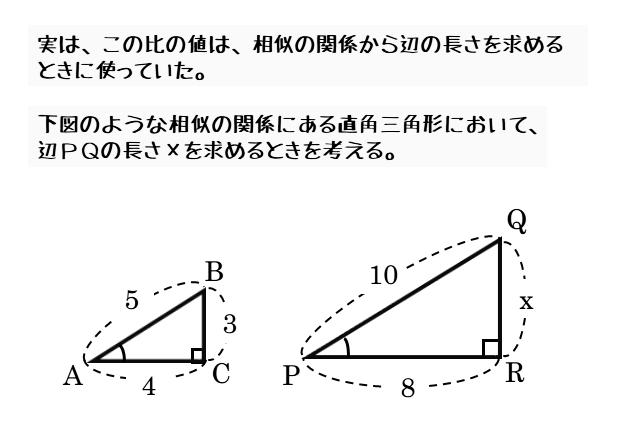
○ 中学校で習ったように,相似図形については対応する辺の長さに「比」は等しいので,図のような直角三角形について (1)黄色で示した上の2個の図については , , の「比」は等しくなります.ここまでで示した「直角三角形の辺の比」という定義では、角度θは$0\theta{\pi\over 2}$でなくてはいけない。ではθが${\pi\over2}$を超えた(ただしまだπは超えてない)場合は$\sin\theta,\cos\theta$は値がないのかというと、ここで 定義を拡張する ことでθが${\pi\over2}$を超えても大丈夫なようにする。 直角三角形とは、1つの角が直角(90°)である三角形のことです。 その他の2つの角は90°より小さい鋭角です。 また、直角の向かい側の辺(対辺)のことを 斜辺 といいます。



1




北辰塾 情報局 直撃 中学入試問題 第150回 法政大学第二 辺の比と面積比 直角三角形の折り曲げ
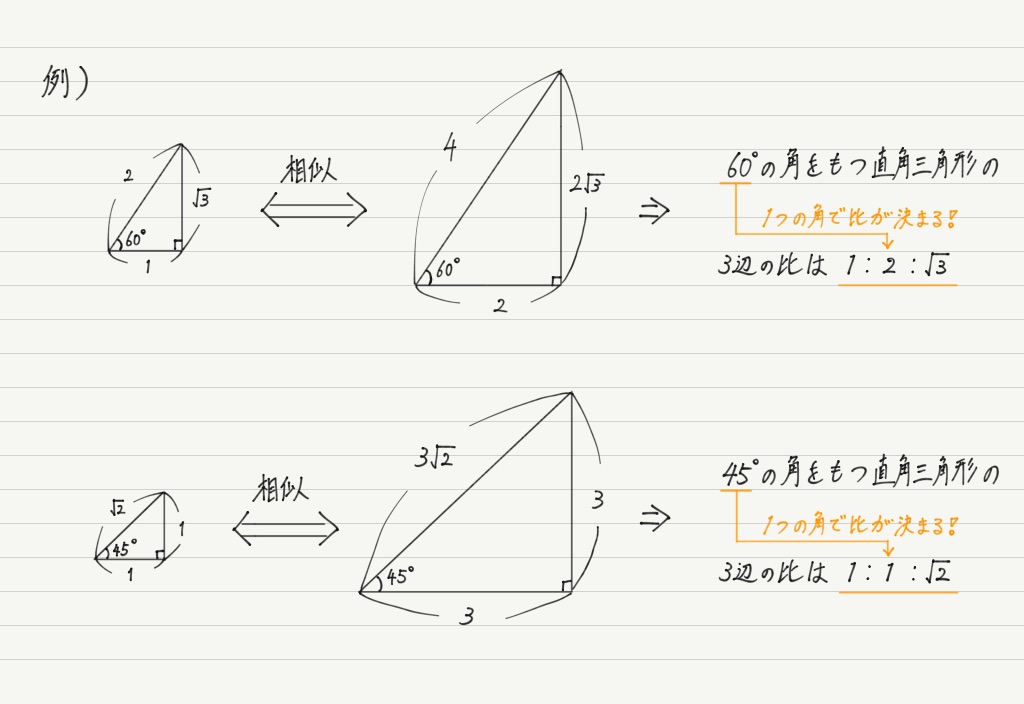
直角を含まない三角形 abc を図に 示した。この三角形の要素,つまり辺の長さと 角の大きさの間の関係式をどうやって発見し たらよいだろうか。前の節で直角を含む場合は 三角比の定義式が要素間の関係式になってい ることを観察したばかりである。相似な三角形の辺の比は等しいので、30°、60°、90°の直角三角形であれば、その3辺の比は $12\sqrt{3}$ であることが分かります。 以上が、代表的な 2 つの直角三角形の辺の比と、それを三平方の定理から求める手順です。 みゆの魔法 その1 三角形の辺の比 $$$$ みんな大好き(?)ピタゴラス数 ピタゴラス数といえば、直角三角形の3辺の長さが整数となるような3つの整数の組のことですね。長さの比率が整数比つまり有理数比な直角三角形はピタゴラス三




二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web
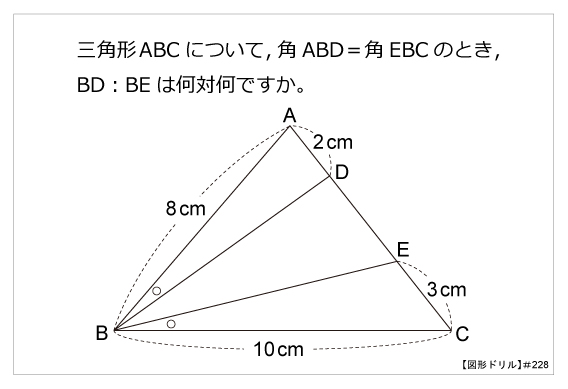



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
5)という比を使っても直角三角形はでき ますが、簡単に √ 5という比はなかなか作れません。3辺の比が整数の直角3角形 があれば、このように、いろいろと便利なことがありますが、他に3辺の比が整数 となる直角3角形はできるのでしょうか?}{ 11\sqrt{ 2 } }\)になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。 三角形の中でも直角三角形のみの辺の比ってのが1個のポイントですかね。 直角三角形は3つの角のうち、1つの角が直角 (90度) です。三角比はこの 直角以外の角度が1つでも分かれば、3辺の長さの比率が分かる っていう優れものです。



雑談 解答 辺の長さが整数比である直角三角形は いくつありますか 隠し味 鷹の爪 意味はありません
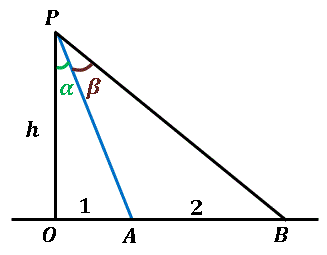



角度比の極限値 底辺を円弧とみなせば
特別な直角三角形の辺の長 さの比 ・ウ 特別な直角三角形の3辺の比を利用して、い ろいろな長さを求めることができる。ワークシ ート記述の観察 第6時 三平方の定理を ~ 第7時 利用した問題を 解くことができ 2点間の距離を求めること第296問 b辺の比と直角 図形ドリル 5年生 6年生 三角形 直角 辺の比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題をケプラー三角形 は、面積が 黄金比 を公比とした等比数列の関係になっている3つの正方形の辺で形成される直角三角形。 ケプラー三角形 は三辺の比が 等比数列 となっている 直角三角形 で、その公比は




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト
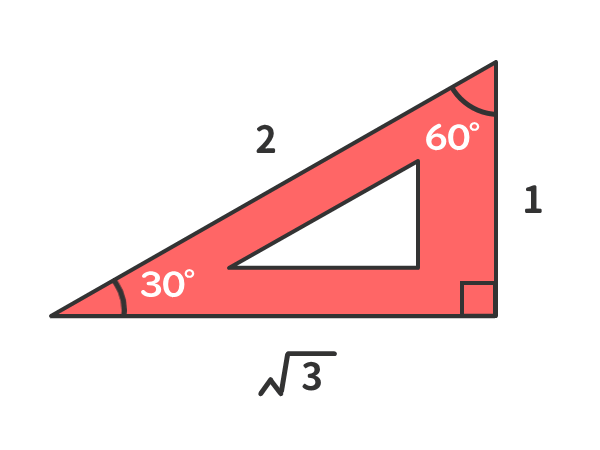
次の3つの直角三角形の辺の比を覚えてください。 30° 60° 90°の直角三角形の辺の比 この形はは三角定規の三角形です。正三角形の半分になります。(正三角形の高さを求めるのにも利用します。) 12√3 をしっかり覚えてください。
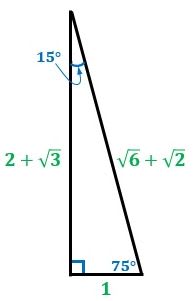



直角三角形の辺の比 東久留米 学習塾 塾長ブログ
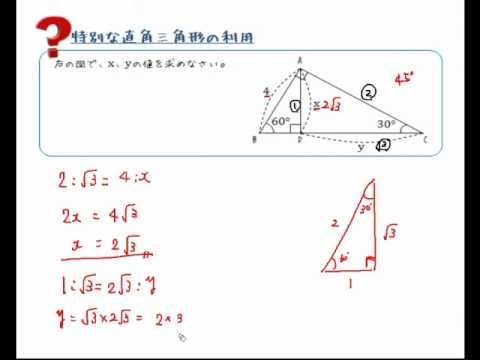



特別な直角三角形の利用 Youtube
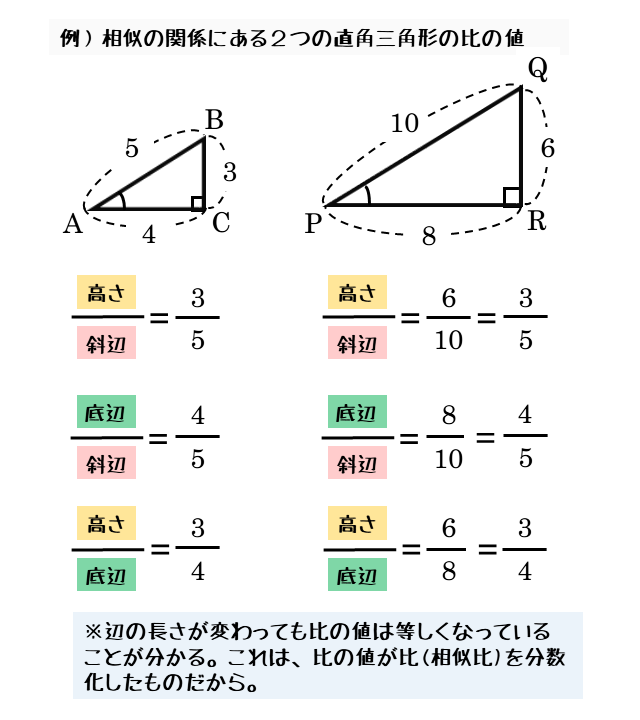



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題




中学受験 直角三角形の相似問題 内接する正方形の一辺の長さは




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



直角三角形の辺の比 東久留米 学習塾 塾長ブログ



1




直角三角形 Wikipedia




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



直角三角形の3辺の比について 1 2 3とありますが2と 3の位置 Yahoo 知恵袋




タンジェントとは何か 中学生でも分かる三角関数の基礎



数i 基本的な三角比の値




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
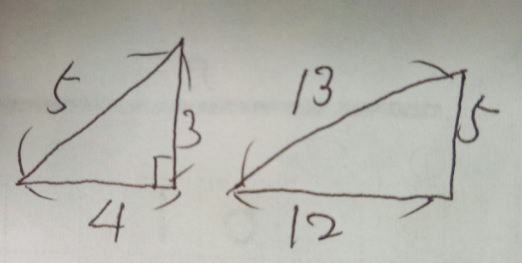



直角三角形の相似 3 4 5 5 12 13 中学受験 塾なし




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明
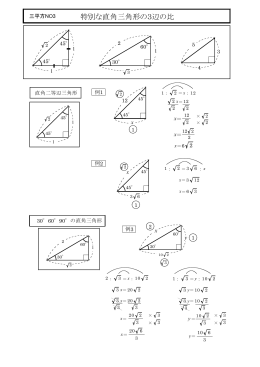



特別な直角三角形の3辺の比



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ The 2nd



Pr この広告は3ヶ月以上更新がないため表示されています ホームページを更新後24時間以内に表示されなくなります 三平方の定理 三平方の定理とは 三平方の定理 ピタゴラスの定理 定理 任意の直角三角形において 斜辺の長さの自乗は他



Www Kyo Kai Co Jp Img Support Motto Motto5 Pdf



3




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三平方の定理 覚えておきたい基本公式を解説 数スタ




テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア




3 4 5の三角形で 本当に直角ができる Note Board




高校数学 直角三角形と長さの比 練習編 映像授業のtry It トライイット



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




標準 2つの直角三角形に分解して三角比を求める なかけんの数学ノート



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
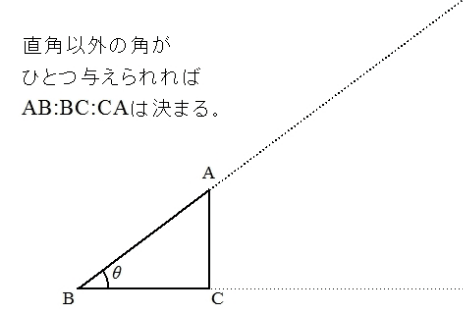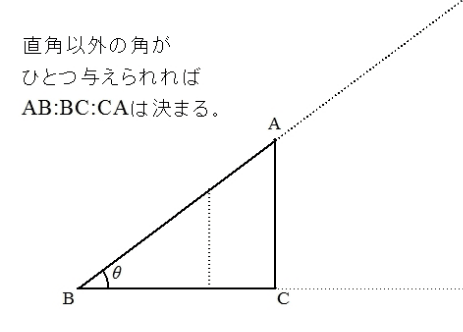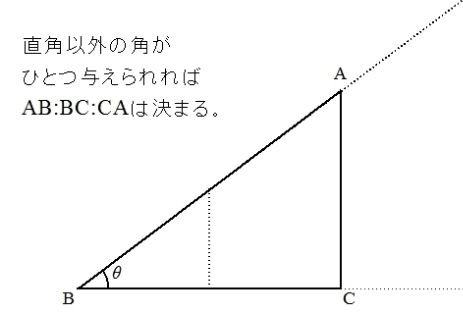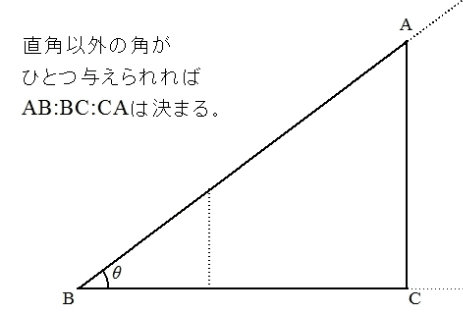



三角比とは 定義の意味やポイントについて 発想の原点は 相似 にあり ここからはじめる高校数学




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理の証明と使い方
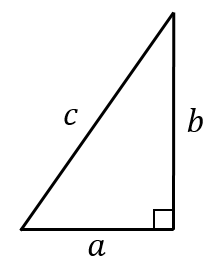



直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
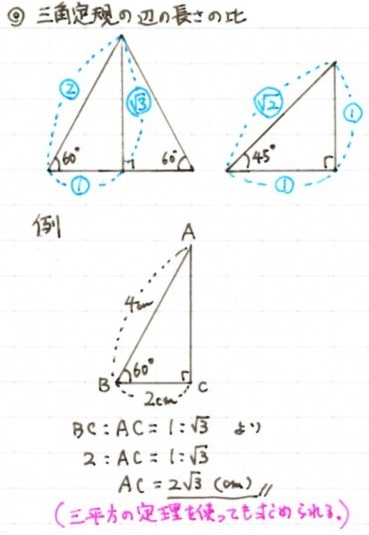



直角三角形の3辺の比 高校入試問題 数学 を毎日解いてみよう




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー
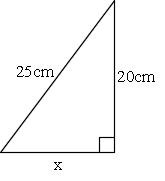



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
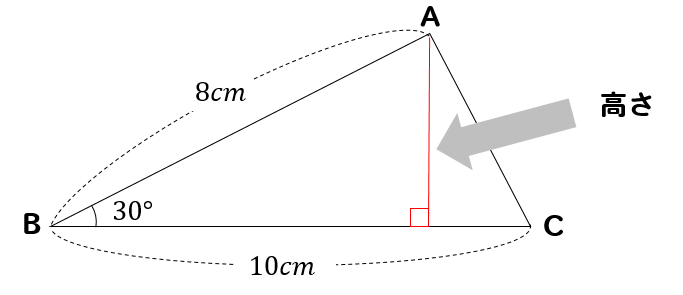



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア



1




直角三角形による三角比の定義 三角関数 高校数学 しらたきおじさんの学問帳




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
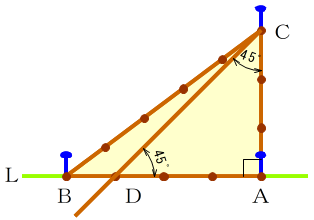



3 4 5の三角形で 本当に直角ができる Note Board



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




高校数学 直角三角形と長さの比 例題編 映像授業のtry It トライイット




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




辺の比と面積比 基本編 Youtube



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ




三角比 30 45 60 もう一度やり直しの算数 数学
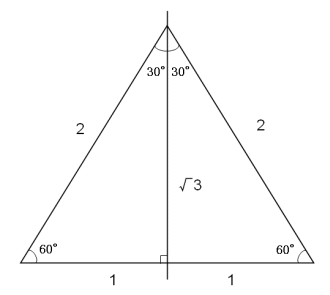



初等幾何 正三角形がつくる直角三角形 大人が学び直す数学
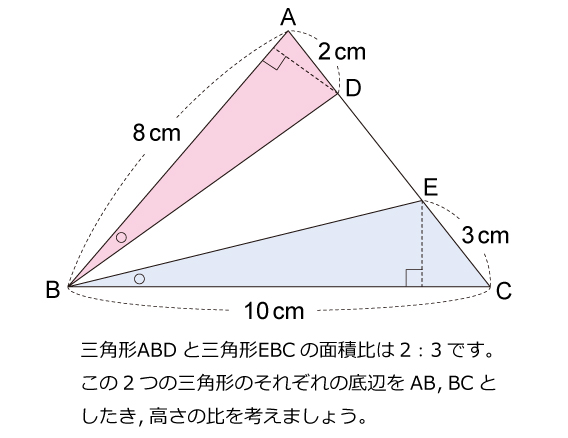



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext




特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてください Clear




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




直角三角形の辺の長さ 合同条件 面積について アタリマエ
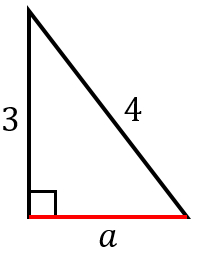



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
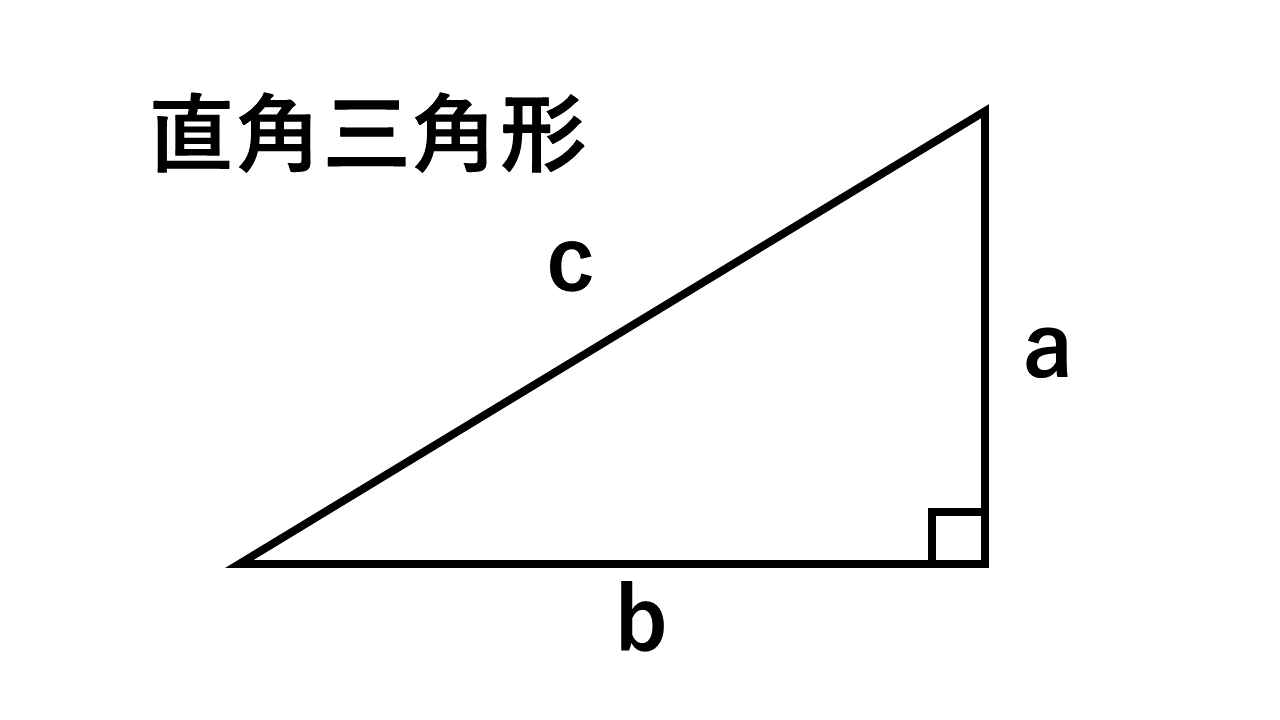



中学数学 直角三角形3 4 5以外に知ってる



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



3 4 5と1 2 3と3角定規とtvと黄金比と 万象酔歩




直角三角形の角から垂線を引いたときの底辺の比の問題 の裏ワザ 大阪のプロ家庭教師が できない を できる に変える




三平方の定理の証明と使い方
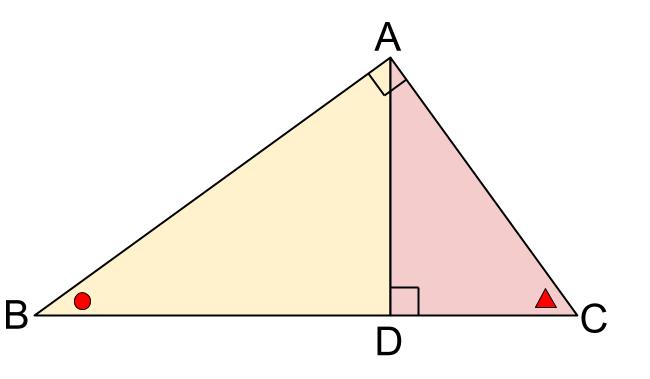



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
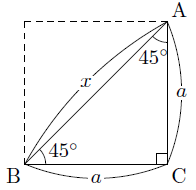



三角定規の3辺の比 まなびの学園




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
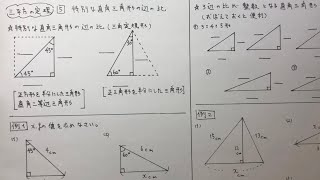



中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




直角三角形の辺の比と角度 そらいろ日記 言葉の宝箱




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



数i 基本的な三角比の値




特別な直角三角形の辺の比 無料で使える中学学習プリント
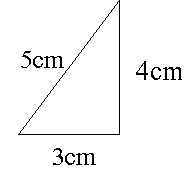



三角形の性質




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿